Introduction
Within this tutorial, we will provide a beginner’s guide to subnetting. Before we dive into subnetting we will look into the structure of an IP address, along with some of the key IP schemes that assist in modern day IP subnetting.
Note: The scope of this document covers IPv4 subnetting only.
What is IP?
IP is a connectionless protocol that operates at the network layer of the OSI model. IP enables communication between hosts by carrying data within packets. Each host is assigned an IP address which is used to ensure that traffic is sent to the correct destination, synonymous in many ways to a postal address that we place on a letter.
Addressing
An IP address (in the case of v4) is built upon 32-bits, expressed in four numbers known as octets. Each octet is 8 bits i.e one byte.
Each address is made up of 2 identifiers (shown below):
- Network - the network the IP address belongs to. For example the street name.
- Host - the host identifier of the device for the network. For example the house number.

Figure 1 - IP Address.
To determine which parts of an IP address are the network bits, and which are host bits, a subnet mask is used. Within a subnet mask, the sequential bits that are on (1) are deemed the network bits and the bits that off (0) are considered the host bits. For example, 255.255.0.0 would result in the first 2 octets (16bits) being the network bits and the remainder being the host bits.
Classes
When the IP protocol was first released it was built upon a classful addressing architecture. This architecture provided three different network classes - known as class A, B and C. Each class provided a different subnet mask based upon the IP range.
| Class | 1st Octet Bits | Range | Mask |
| A | 0 | 0.0.0.0 – 126.255.255.255 | 255.0.0.0 |
| B | 10 | 128.0.0.0 – 191.255.255.255 | 255.255.0.0 |
| C | 110 | 192.0.0.0 – 223.255.255.255 | 255.255.255.0 |
| Class | Mask | Range | Range Prefix | Binary |
| A | 255.0.0.0 | 10.0.0.0–10.255.255.255 | /8 | 00001010.00000000.00000000.00000000 |
| B | 255.255.0.0 | 172.16.0.0–172.31.255.255 | /12 | 10101100.00010000.00000000.00000000 |
| C | 255.255.255.0 | 192.168.0.0–192.168.255.255 | /16 | 11000000.10101000.00000000.00000000 |
However, this was hugely inefficient, should a company require 2 IP addresses for a point to point link then the smallest classful network that could be assigned was a class C network, which would provide 256 hosts. As you can see this was a huge waste.
CIDR/VLSM
With the explosion of the internet and the need to address more and more devices, this issue was compounded and a solution was required.
The solution to this issue came in the form of - Classless Inter-Domain Routing (CIDR) and Variable Length Subnet Masking (VLSM). Both of which are key to modern day subnetting.
Classless Inter-Domain Routing (CIDR)
CIDR (as per RFC1519) was implemented to allow the routing of both classful and classless networks. Classless networks do not use the subnet masks mandated by the different A, B or C classes, instead, the subnet mask (aka CIDR “bit” notation) is represented - ranging from /8 to /32.
This allowed networks to be aggregated, reducing the number of entries in the IP routing tables, whilst also allowing for greater efficiency in IP route processing.
Variable Length Subnet Masking (VLSM)
VLSM is the "subnetting of subnets," which means that VLSM allows network engineers to divide an IP address space into a hierarchy of subnets of different sizes, making it possible to create subnets with very different host counts without wasting large numbers of addresses.[1]
Subnetting Overview
First of all - what is subnetting?
A subnetwork or subnet is a logical subdivision of an IP network.The practice of dividing a network into two or more networks is called subnetting.[2]
Subnetting provides us with a number of benefits, such as:[3]
- Conserving IP addresses.
- Reducing networking traffic (i.e BUM).
- Simplifying the network design.
If you recall, we previously spoke about an IP address having a network and host identifier. Subnetting works by taking bits from the host part of an IP address in order to create subnet identifier bits (shown below). We then use these subnet bits to calculate the number of additional subnets available.
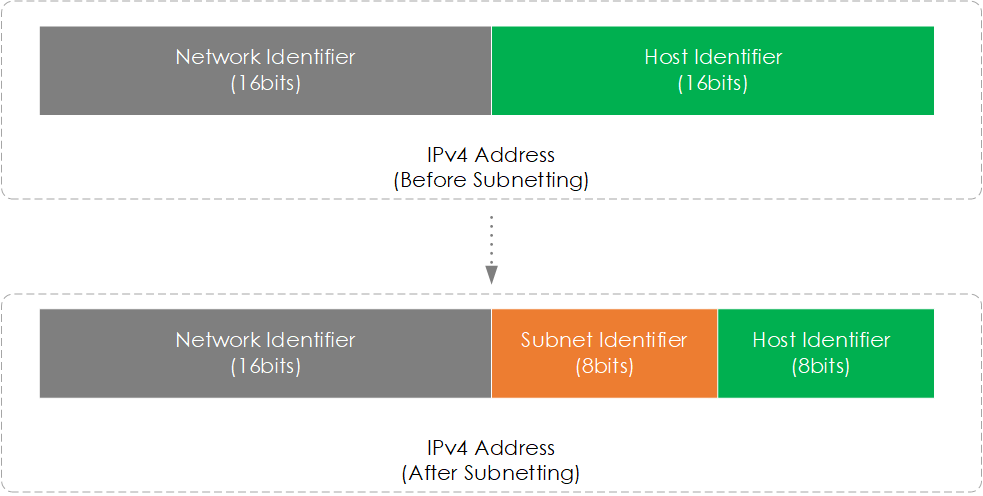
Figure 2 - Subnetting.
How to Subnet w/ Examples
In order to show how subnetting is performed, I will step through a number of examples. I won't go into full-blown explanations I will cut straight past the BS, to the calculations. Boom!
Before we begin, it is worth mentioning that I will use a technique that uses something known as the magic number.
The Magic Number
The magic number is simply the decimal representation of the host bits (in red).
Example:
IP Address = 192.168.1.22
Subnet Mask = /26 or 255.255.255.192
Magic Number: 256 - 192 = 64
We will now use the magic number as part of our examples. Let's go…
Subnet Mask Chart
Here is a quick reference table for help when subnetting.
| Subnet Mask | CIDR | Binary Notation | Network Bits | Host Bits | Available Addresses |
| 255.255.255.255 | /32 | 11111111.11111111.11111111.11111111 | 32 | 0 | 1 |
| 255.255.255.254 | /31 | 11111111.11111111.11111111.11111110 | 31 | 1 | 2 |
| 255.255.255.252 | /30 | 11111111.11111111.11111111.11111100 | 30 | 2 | 4 |
| 255.255.255.248 | /29 | 11111111.11111111.11111111.11111000 | 29 | 3 | 8 |
| 255.255.255.240 | /28 | 11111111.11111111.11111111.11110000 | 28 | 4 | 16 |
| 255.255.255.224 | /27 | 11111111.11111111.11111111.11100000 | 27 | 5 | 32 |
| 255.255.255.192 | /26 | 11111111.11111111.11111111.11000000 | 26 | 6 | 64 |
| 255.255.255.128 | /25
|
11111111.11111111.11111111.10000000 | 25 | 7 | 128 |
| 255.255.255.0 | /24 | 11111111.11111111.11111111.00000000 | 24 | 8 | 256 |
| 255.255.254.0 | /23 | 11111111.11111111.11111110.00000000 | 23 | 9 | 512 |
| 255.255.252.0 | /22 | 11111111.11111111.11111100.00000000 | 22 | 10 | 1024 |
| 255.255.248.0 | /21 | 11111111.11111111.11111000.00000000 | 21 | 11 | 2048 |
| 255.255.240.0 | /20 | 11111111.11111111.11110000.00000000 | 20 | 12 | 4096 |
| 255.255.224.0 | /19 | 11111111.11111111.11100000.00000000 | 19 | 13 | 8192 |
| 255.255.192.0 | /18 | 11111111.11111111.11000000.00000000 | 18 | 14 | 16384 |
| 255.255.128.0 | /17 | 11111111.11111111.10000000.00000000 | 17 | 15 | 32768 |
| 255.255.0.0 | /16 | 11111111.11111111.00000000.00000000 | 16 | 16 | 65536 |
| 255.254.0.0 | /15 | 11111111.11111110.00000000.00000000 | 15 | 17 | 131072 |
| 255.252.0.0 | /14 | 11111111.11111100.00000000.00000000 | 14 | 18 | 262144 |
| 255.248.0.0 | /13 | 11111111.11111000.00000000.00000000 | 13 | 19 | 524288 |
| 255.240.0.0 | /12 | 11111111.11110000.00000000.00000000 | 12 | 20 | 1048576 |
| 255.224.0.0 | /11 | 11111111.11100000.00000000.00000000 | 11 | 21 | 2097152 |
| 255.192.0.0 | /10 | 11111111.11000000.00000000.00000000 | 10 | 22 | 4194304 |
| 255.128.0.0 | /9 | 11111111.10000000.00000000.00000000 | 9 | 23 | 8388608 |
| 255.0.0.0 | /8 | 11111111.00000000.00000000.00000000 | 8 | 24 | 16777216 |
Examples
Calculate the next 5 Networks
Question
What are the next 5 networks from 30.0.100.10/28?
Calculation
Our answer is calculated via the following steps:
- The magic number is 16 (/28 == 255.255.255.240 ; 256-240 == 16).
- How many 16’s fit into 30.0.100.10 = 0.
- Therefore the first network is 30.0.100.0.
- Keep adding the magic number to obtain the next network.
Answer:
The following 5 networks are:
30.0.100.16
30.0.100.32
30.0.100.48
30.0.100.64
30.0.100.80
Calculate the Total Available Subnets
Question
How many subnets and hosts per subnet can you get from the network 172.30.0.0 255.255.255.240?
Calculation
Our answer is calculated via the following steps:
- Calc the subnet bits. 172.30.0.0/28:
- Net bits = 16bits.
- Host bits = 4bits.
- Subnet bits = 12bits.
- The total subnets is 4096 (based on 12bits)
- The total hosts per subnet.
- Lets us the magic number. 256 - 240 = 16.
- Minus 2 (1 for network number and 1 for broadcast) = 14.
Answer
Total subnets = 4096
Total hosts (per subnet) = 14
Calculate the Valid host Range
Question
What is the valid host range of 172.16.93.193/20 a part of?
Calculation
Our answer is calculated via the following steps:
- The magic number is 16 (/20 == 255.255.240.0 ; 240-256 = 16).
- How many 16’s (magic number) into x.x.93.x? 80
- The network number is 172.16.80.0.
- The broadcast is:
- 3rd octet = 80 + 16 (magic number) - 1 = 95
- 4th octet = 255.
- Network Range is 172.16.80.0-172.16.95.255
Answer
The valid range is 172.16.80.1-172.16.95.254.
Calculate the Subnet
Question
Which subnet does host 172.24.102.208 255.255.255.224 belong to?
Calculation
Our answer is calculated via the following steps:
- The magic number is 32 (x.x.x.224-256).
- How many 32’s in 172.24.102.208? 192
Answer
The subnet is 172.24.102.192.
Calculate the Broadcast Address
Question
What is the Broadcast of 172.30.233.0 255.255.255.128?
Calculation
Our answer is calculated via the following steps:
- The magic number is 128 (x.x.x.128-256).
- How 128’s fit into x.x.x.0? 0
- Next subnet is 172.30.233.128.
- Range of subnet is 172.30.233.0-172.30.233.127.
Answer
Broadcast is 172.30.233.127.
Reference
"What is variable-length subnet mask (VLSM)? - Definition from WhatIs ...." 17 Aug. 2014, https://searchnetworking.techtarget.com/definition/variable-length-subnet-mask. Accessed 7 May. 2019. ↩︎
"Subnetwork - Wikipedia." https://en.wikipedia.org/wiki/Subnetwork. Accessed 7 May. 2019. ↩︎
"Simplify Routing with Subnetting: How to Organize Your Network Into ...." 8 Nov. 2007, https://www.pluralsight.com/blog/it-ops/simplify-routing-how-to-organize-your-network-into-smaller-subnets. Accessed 7 May. 2019. ↩︎